Algorithm. Dynamic Algorithm 

[Visual Studio과 C#으로 구현/동적계획알고리즘]

Algorithm Dynamic Algorithm Coding // Week10

20211111_20615034

[ Dynamic Algorithm  Coding_Theory ]

 피보나치, 타일링, Floyd-Warshall

- 동적계획 알고리즘 정의

최적화 문제를 해결하는 알고리즘

- 문제 해결방법

입력크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결. 최종적으로 원래 주어진 입력의 문제를 해결.

- 동적 계획 알고리즘의 예시

피보나치 수열의 재귀적 해법

Fibo(n) {

  if(n == 1) return 1;

  if(n == 2) return 1;

  return Fibo(n-1) + Fibo(n-2);

}

=> 시간 복잡도 = O(2N)

같은 방법을 너무 많이 적용하게 되어 매우 비효율적인 연산이 진행 됨.

예를 들어 n = 7인 경우에는 Fibo(6)과 Fibo(5)가 파생되는데 Fibo(6)이 실행 되면 다시 Fibo(5)와 Fibo(4)가 시행

이 때, Fibo(5)가 두번 연산되는 것을 볼 수 있고 이는 재귀적으로 호출하면 할수록 더 많은 중복이 일어나게 됨. 중복된 연산을 해결에 동적 계획 알고리즘이 사용.

연산되었던 값들은 배열에 저장하고 이를 다음에 사용할 필요가 있는 경우를 if문을 통해 선별하여 사용하게 됨.

- 동적 계획 알고리즘 적용한 피보나치 수열

int d[100];

Fibo(n) {

  if(n == 1) return 1;

  if(n == 2) return 1;

  if(d[n] != 0) return d[n];

  return d[n] = Fibo(n-1) + Fibo(n-2);

}

=> 시간 복잡도(N)

재귀적 단점을 보완, 시간 복잡도 효율성 큼.

[타일링 문제]

- 길이 n인 사각형을 채우기

길이 n-1인 사각형에 2*1 타일을 한 개 붙이는 경우

길이 n-2인 사각형에 1*2 타일 두 개를 가로로 붙인 경우

길이 n-2인 사각형에 타일 두 개를 세로로 붙인 경우(X) => 첫 번째 경우에 포함되어 있음

==> Tile(n) = Tile(n-1) + Tile(n-2)  

- 길이 n인 사각형 채우기 

길이 n-1인 사각형에 2*1 타일을 하나 세로로 붙인 경우

길이 n-2인 사각형에 1*2 타일을 두개 가로로 붙인 경우

길이 n-2인 사각형에 2*2 타일을 하나 붙인 경우

를 다 더한 값과 같다고 할 수 있으므로

==> Tile(n) = Tile(n-1) + 2*Tile(n-2) 

[ Dynamic Algorithm  Coding_Theory ]

 연속 행렬 곱셈

- 연속 행렬 곱셈 문제
연속 행렬 곱셈 문제는 연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제
​
- 행렬의 곱셈
연속된 행렬의 곱셈에는 결합 법칙을 허용(행렬의 곱셈은 이웃하는 행렬끼리만 곱해야 함.)
만약 10*20 행렬 A와 20*5 행렬 B가 있다면 둘의 곱셈에 필요한 곱셈 횟수는 20*10*5 = 1000이 되며 두 행렬을 곱한 결과 행렬 C는 10*5 행렬이 됨.

==> 하나의 타일로 만드는 과정이라 생각하면 이해하기 용이 함.
​
ex) 3개의 행렬을 곱해야 하는 경우 곱셈의 방법은 총 2가지 경우로 나뉨.
 10*20 행렬 A, 20*5 행렬 B, 5*15 행렬 C 일 때,
 A*B*C = (A*B)*C 의 경우

​
- (A*B)의 곱셈 횟수 : 10*20*5 = 1000
- (A*B)의 결과 행렬 : 10*5 행렬 AB

- AB*C의 곱셈 횟수 : 10*5*15 = 750

- AB*C의 결과 행렬 : 10*15 행렬 ABC

=> 최종 결과물 : 10*15 행렬 ABC, 1750번의 곱셈 횟수

- A*B*C = A*(B*C) 의 경우

(B*C)의 곱셈 횟수 : 20*5*15 = 1500

(B*C)의 결과 행렬 : 20*15 행렬 BC

BC*A의 곱셈 횟수 : 15*20*10 = 3000

BC*A의 결과 행렬 : 10*15 행렬 ABC

=> 최종 결과물 : 10*15 행렬 ABC, 4500번의 곱셈 횟수

=> 최소 곱셈 횟수 1750번

- 연속 행렬 곱셈의 동적계획 알고리즘을 통한 문제 풀이

연속 행렬의 곱셈 또한 수행을 거치면서 중복되는 계산이 정말 많이 일어난다. 이를 표에 저장하고 다음에 사용할 때에 끌어다쓰는 방식으로 해결하면 훨씬 수행을 효율적으로 진행할 수 있으며 이를 동적계획 알고리즘의 적용이라고 볼 수 있다.

이 부분은 이론적으로 차례대로 하면 이해가 되는데

너무 오래 걸려서 다음에 이해 더하고 포스팅을 수정하겠음.

[행을 i / 대각선 L / 행 x좌표, 열 y좌표]

- L=1 일 때,

(1,2)의 지점 경우, A1부터 A2까지 곱한 값 기입. 

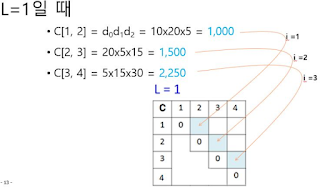
- C[1, 2]

곱셈 횟수가 10*20*5=1000 최종 행렬은 10*5

- C[2, 3] 

곱셈 횟수 : 20*5*15 = 1500 최종행렬 : 20*15

- C[3, 4] 

곱셈 횟수 : 5*15*30=2250 최종행렬 : 5*30

- L=2 일 때,

3개를 곱하는 구조에는 총 2가지 경우를 고려하여 더 적은 곱셈 횟수를 찾아야 함.(L=1에서 계산하였던 값은 그대로 가져와 사용)

- (A1*A2)*A3 

 곱셈 횟수 : 1000(C[1,2], L=1에서 저장되었던 값) + 10*5*15 = 1750

- A1*(A2*A3) 

 곱셈 횟수 : 1500(C[2,3]) + 10*20*15 = 4500

=> C[1, 3] = 1750

- A2*(A3*A4)의 경우

곱셈 횟수 : 20*5*30 + 2250(C[3,4]) = 5250

- (A2*A3)*A4의 경우

곱셈 횟수 : 1500(C[2,3]) + 20*15*30 = 10500

=> C[2, 4] = 5250

- L=3 일 때,

총 3가지 경우 고려

- A1*(A2*A3*A4)

곱셈 횟수 : 10*20*30 + 5250(C[2,4]) = 11250

- (A1*A2)*(A3*A4)

곱셈 횟수 : 1000(C[1,2]) + 2250(C[3,4]) + 10*5*30 = 4750

- (A1*A2*A3)*A4

곱셈 횟수 : 1750(C[1,3]) + 10*15*30 = 4500 = 6250

=> C[1,4] = 4750

== A1*A2*A3*A4 연속 곱셈 행렬의 최소 곱셈 횟수 = 4750

연속 행렬 곱셈 문제를 위와 같이 동적 계획 알고리즘을 이용하여 풀이시, 효율적으로 진행 됨. 기존의 행렬 곱셈 연산 방식을 시간복잡도로 표현하면 2^n을 n^3 으로 바꿔 줌.

· 총 부분 문제의 수 : (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2

· 하나의 부분 문제는 k-루프가 최대 (n-1)번 수행

=> 시간 복잡도 : O(n2) x O(n) = O(n3)